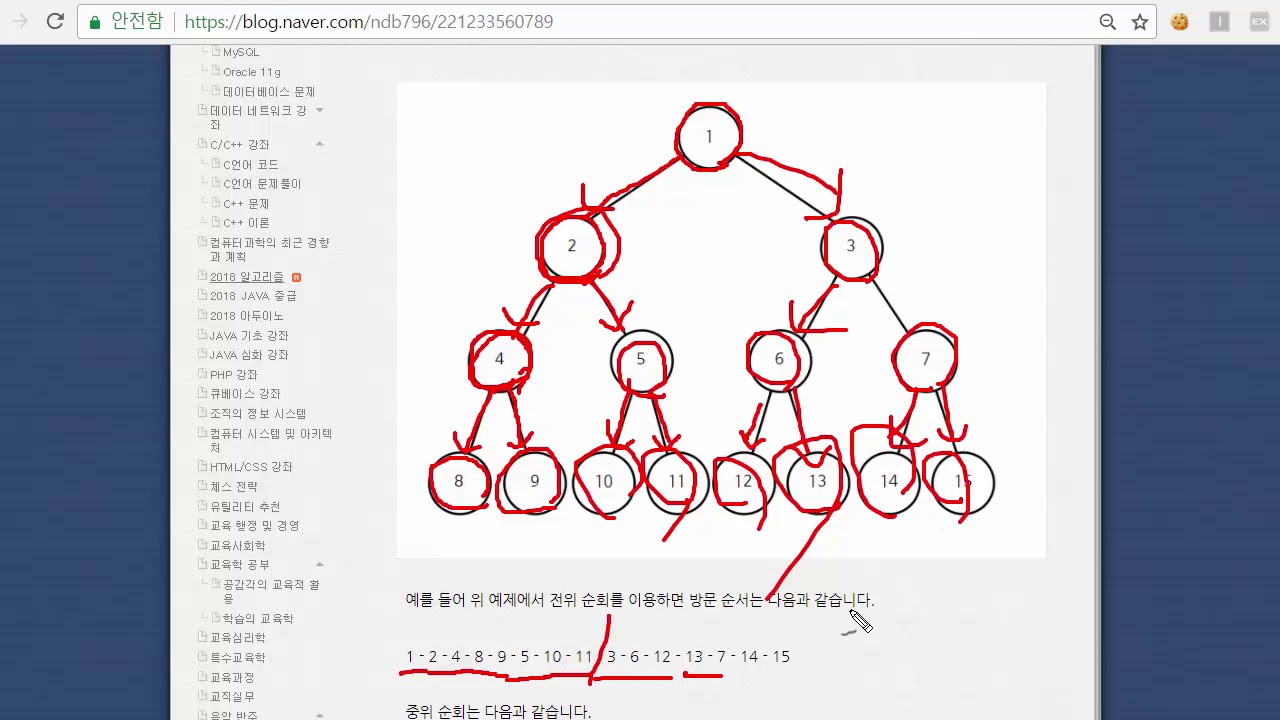
Practical Algorithmic Course - Day 10

1. Binary Tree ◆ This is the most representative structure of conceptual nonlinear data. This structure is used to speed up the search for data. If it is not completely binary, it should be implemented using a pointer. This is because it has a free tree structure that cannot be expressed in an array. At this time, there are three main patrol structures.1. Preorder Traversal (self-handling – >) Left child visit -> Right child visit) 2. Inorder Traversal (Left Child Visit – >) Right child visit) 3. Postorder Traversal (visiting left child – >) Visit Right Child – > Take care of yourself) – > Mathematical expressions are most often used to make them easier for computers to understand.

2. Dynamic Programming ◆ Conceptual DP, also known as dynamic programming, is an algorithm that solves one problem only once.The disadvantage of dividing and conquering techniques is that they solve the same problem many times. Fibonacci sequence (no disadvantages for elements such as alignment). ex)Therefore, DP can be used under two assumptions.1. You can divide big problems into small ones.2. The answer to a small question is the same for a big question including it.It’s very similar to the divisional conquest technique, but the biggest difference is that Memoization is used. In other words, the correct answer is saved in a data structure such as an array without finding it again, and only that value is returned later if necessary.◆ Example (Fibonacci sequence) Implement as a recursive function

인기글

#stdio <stdio。h>int fibo(int x) {if(x == 1 または x==2) return 1;fibo(x-1) + fibo(x-2);} int main(interval) {printf440%d”,printo(50));}

Implemented in DP (using recursive functions)

#stdio <stdio。h>unsigned int dp[101]= {0,}; unsigned into fibo(int x){if(x == 1 or x==2) return 1;if(dp[x]!= != 0) return dp[x]; return dp[x]= fibo(x-1) + fibo(x-2);} int main(vline){printf440%u”,vo(50));};};};};}

Implemented in DP (using repeat doors)

#stdio <stdio。h>int main(int main){nsigned int dp[100]={0,};nt num = 50;p[1]= 1;p[2]= 1;for (int i=3;i <=num;++i) {p[i] = = dp[i-1] + + dp[i-2]} printf440%u”,dp[40]);}

#stdio <stdio。h>int main(int main){nsigned int dp[100]={0,};nt num = 50;p[1]= 1;p[2]= 1;for (int i=3;i <=num;++i) {p[i] = = dp[i-1] + + dp[i-2]} printf440%u”,dp[40]);}